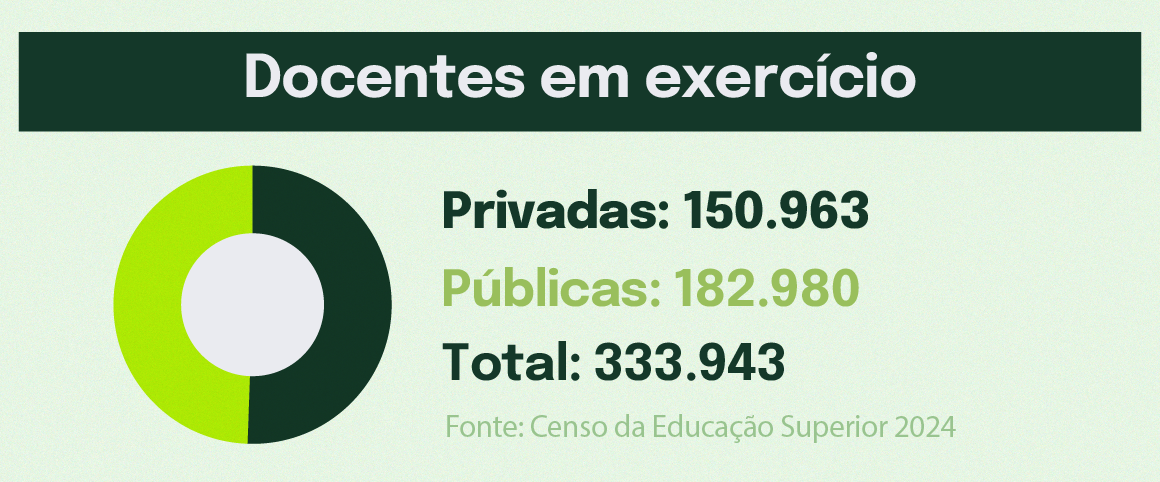
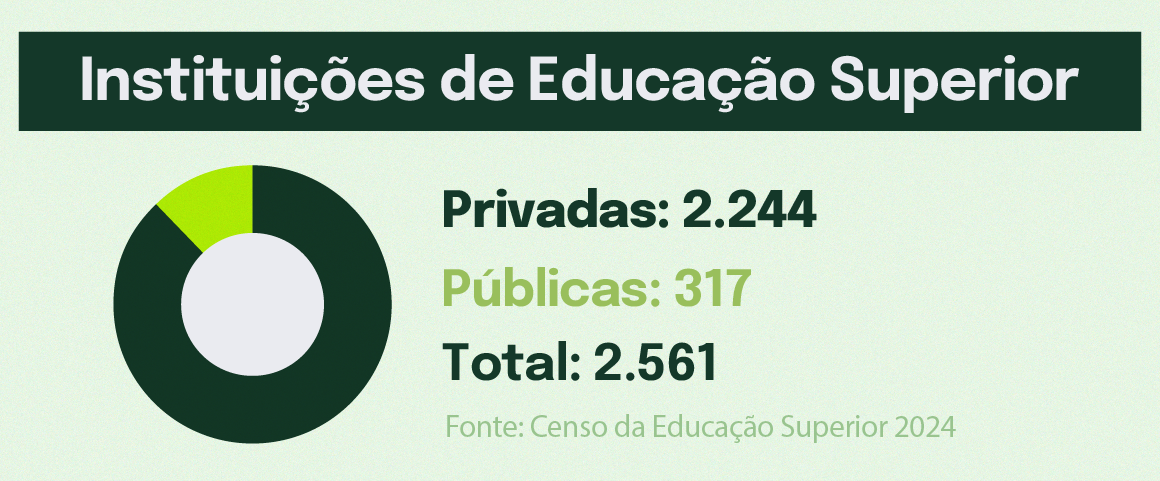
Nenhum ser humano conhece em detalhes todas as tecnologias atualmente disponíveis. No entanto, tão verdadeiro quanto essa afirmação é o fato de que que todos, sem exceção, podem ter alguma noção básica de tudo o que já foi desenvolvido até aqui. Conectar o altamente complexo estado da arte da ciência e da tecnologia às possibilidades de aprendizagem cotidiana de cada um de nós é uma tarefa que envolve a capacidade de decifrar, de forma didática, conceitos extremamente sofisticados. Essa é a essência da divulgação científica, a qual exige letramento, especialmente matemático.

Machine learning ou “aprendizagem de máquina” é um dos principais pilares da inteligência artificial (IA). Trata-se de desenvolver sistemas capazes de aprender com dados, identificando padrões e tomando decisões com mínima, ou nenhuma, intervenção humana. Para ilustrar esse conceito, podemos pensar no clássico “jogo da velha”, que possui um tabuleiro com nove casas. Dois jogadores, alternadamente, colocam círculos (Os) ou cruzes (Xs). Quem completar com três símbolos iguais uma linha, coluna ou diagonal inteira ganha a partida.

Donald Michie (1923-2007), carinhosamente conhecido como “Duckmouse”, foi colega de Alan Turing (1912-1954), o pai da Ciência da Computação, e juntos decifraram o código da máquina “Enigma”, ajudando os Aliados a vencerem a Segunda Guerra Mundial (1939-1945). Em 1961, ele criou uma engenhosa IA chamada MENACE, um sistema baseado em caixas de fósforo e missangas de cores diversas (aqui usamos números), propiciando uma visão simples acerca de aprendizagem de máquina. No total, eram suficientes 304 caixas de fósforos, que representavam diferentes possibilidades de arranjos ao longo do jogo. Ele denominou seu sistema de Machine Educable Noughts and Crosses Engine (em português, “Jogo da Velha Educável por Máquinas”).

Iniciemos por numerar os nove quadrados do tabuleiro, começando do primeiro quadrado no vértice superior esquerdo (1), caminhando da esquerda para a direita e de cima para baixo, até o último quadrado no vértice inferior direito (9). Por hipótese, a máquina joga primeiro, via sorteio, e o humano, com escolha a critério dele,  joga na sequência,  e assim por diante.

Os quadrados do tabuleiro podem ser classificados, de forma reduzida, em três tipos de “estados”: os extremos (1, 3, 7, 9), os lados (2, 4, 6, 8) e o centro (5). A máquina inicia jogando, escolhendo por sorteio um desses três estados, restando ao humano fazer o segundo lance. Imagine que a máquina, representada aqui por caixas de fósforo com os novos números de 1 a 9 dentro, sorteou  começar com 1 (mesmo raciocínio se aplicaria se fossem as casas 3, 7 ou 9), o humano poderá escolher qualquer um dos demais 8 quadrados. Se escolher as casas 2 ou 4 resultam configurações idênticas, bem como 3 e 7, e da mesma forma 6 ou 8. Esses 3 arranjos distintos somados às possibilidades de escolher 5 ou de escolher 9, formam 5 possibilidades no total (por favor, convença-se disso antes de seguir adiante). Observe agora que, se ao invés de 1, a máquina tivesse sorteado 3, 7 ou 9 seria o mesmo raciocínio, restando portanto 5 configurações em qualquer um desses casos (em outras palavras, precisamos de 5 caixinhas de fósforo para tratar desses estados por ocasião do segundo lance).

Por sua vez, se a máquina tivesse inicialmente sorteado a quadrado 2 para primeiro lance, restaria ao humano a escolha entre todos os quadrados menos 2, porém, as casas 1 e 3, bem como 4 e 6 ou 7 e 9, seriam idênticas, formando, por enquanto, 3 configurações distintas. Somados às possibilidades das escolhas de 5 ou de 8 (mais duas novas configurações), teríamos 5 possíveis estados neste caso. Observar que se, ao invés de 2, a máquina tivesse sorteado  4, 6 ou 8, a história seria a mesma, portanto, bastam mais 5 caixinhas de fósforo para descrever essas novas 5 possibilidades. 

Finalmente, restou à máquina ter de início sorteado o único ainda não escolhido, o 5. Neste caso, o lance do humano caso fossem as casas 2, 4, 6 ou 8 resultaria algo semelhante, portanto, temos, neste caso, somente um novo estado. Igualmente, se o humano escolhesse 1, 3, 7 ou 9 também seria mais um novo estado. Portanto, a escolha inicial do 5 gera a possibilidade de mais dois estados no segundo lance. Somando às 10 abordagens acima descritas (5 para iniciar por 1 ou semelhantes mais 5 iniciando por 2 ou equivalentes) precisamos, no total, de 12 caixinhas de fósforo para descrever 12 histórias distintas referentes aos dois lances iniciais.

Se seguirmos adiante, com a máquina fazendo o terceiro lance e o humano fazendo o quarto, mais 108 caixas de fósforo seriam necessárias para descrever as possibilidades em direção ao quinto movimento. E assim por diante, lembrando que a máquina, ao jogar por sorteio, caso a caixinha escolhida já esteja preenchida, ela joga de novo (outro número é sorteado de dentro da caixa) até que resulte um espaço vazio preenchível.  

Ao final, seguindo nessa sequência (o raciocínio é sempre o mesmo), alguém ganha (máquina ou humano) ou empatam (quando nenhum dos dois obteve uma sequência de círculos ou cruzes). Neste momento começa o aprendizado de máquina, utilizando algo que se assemelha ao que conhecemos hoje como backpropagation (em português, “retropropagação”, um algoritmo utilizado para treinar redes neurais artificiais) . Caso a máquina tenha perdido (bastante provável ao início) na primeira rodada,  de trás para a frente até caixinha primeira, para cada caixa de fósforo, que originalmente continha 9 números ocultos dentro, retira-se o número sorteado fora (a caixa fica com 8 números diferentes para a segunda rodada). Se houve empate, realizamos o mesmo processo acrescentando o número sorteado, o qual fica duplicado na caixa, agora com 10 números para a próxima rodada. Se a máquina venceu, incluímos mais 3 do número sorteado, restando 12 possibilidades dentro da caixa, sendo que 4 duplicados.

Assim, conforme acima descrito, temos o algoritmo conhecido hoje como “aprendizagem por reforço”, ou seja, a receita que devemos operar nas caixinhas de fósforo. Finda a segunda rodada, vamos para a terceira e assim por diante. Duckmouse demonstrou que após 20 rodadas, ou mais se necessário, a máquina não perde para nenhum humano. Ou seja, ela está treinada.

Podemos acrescentar ao jogo uma possibilidade muito atual. Imagine que do lado de lá, como oponente, não seja mais um humano, mas sim uma outra máquina (outro conjunto de caixas de fósforo). Raciocínio semelhante pode ser desenvolvido, a partir agora do segundo lance, e o resultado final, após um conjunto de rodadas, é bastante provável: o empate. Porém, a novidade é que teremos um outro resultado embutido: duas máquinas treinadas. Observe que adentramos uma nova área, onde uma IA ensina a ela mesma, dispensando, por completo, humanos. Tal lógica, assustadora para alguns, está por trás do treinamento realizado pelo AlphaGo e AlphaZero/Google em 2016 e 2017, bem como pelo DeepSeek-R1-Zero em 2025.

Em resumo, obviamente, os sistemas de IA em aplicação atualmente são muito mais complexos e sofisticados do que este toy model (“modelo de brinquedo”). Porém, o que deve restar do texto é a possibilidade da aprendizagem dos conceitos envolvidos. Se é possível entender algo simples, em tese, com mais esforço e com muito mais ferramentas matemáticas, sempre será razoável ter uma noção acerca de como funciona qualquer IA que usamos no presente ou que utilizaremos no futuro.